Phi φ Accrual Failure Detection
One of the most important virtues of any distributed system is its ability to detect failures in any of its subsystems before things go havoc. Early detection of failures helps in taking preventive actions and ensuring that the system stays fault-tolerant. The conventional way of failure detection is by using a bunch of heartbeat messages with a fixed timeout, indicating if a subsystem is down or not.
In this essay, we take a look into an adaptive failure detection algorithm called Phi Accrual Failure Detection, which was introduced in a paper by Naohiro Hayashibara, Xavier Défago, Rami Yared, and Takuya Katayama. The algorithm uses historical heartbeat information to make the threshold adaptive. Instead of generating a binary value, like conventional methods, it generates continuous values suggesting the confidence level it has in stating if the system crashed or not.
Conventional Failure Detection
Accurately detecting failures is an impossible problem to solve as we cannot ever say if a system crashed or is just very slow in responding. Conventional Failure Detection algorithms output a boolean value stating if the system is down or not; there is no middle ground.
Heartbeats with constants timeouts
The conventional Failure Detection algorithms use heartbeat messages with a fixed timeout in order to determine if a system is alive or not. The monitored system periodically sends a heartbeat message to the monitoring system, informing that it is still alive. The monitoring system will suspect that the process crashed if it fails to receive any heartbeat message within a configured timeout period.
Here the value of timeout is very crucial as keeping it short means we detect failures quickly but with a lot of false positives; and while keeping it long means we reduce the false positives but the detection time takes a toll.
Phi Accrual Failure Detection
Phi Accrual Failure Detection is an adaptive Failure Detection algorithm that provides a building block to implementing failure detectors in any distributed system. A generic Accrual Failure Detector, instead of providing output as a boolean (system being up or down), outputs the suspicion information (level) on a continuous scale such that higher the suspicion value, the higher are the chances that the system is down.
Detailing φ
We define φ as the suspicion level output by this failure detector and as the algorithm is adaptive, the value will be dynamic and will reflect the current network conditions and system behavior. As we established earlier - lower are the chances of receiving the heartbeat, higher are the chances that the system crashed hence higher should be the value of φ; the details around expressing φ mathematically are as illustrated below.
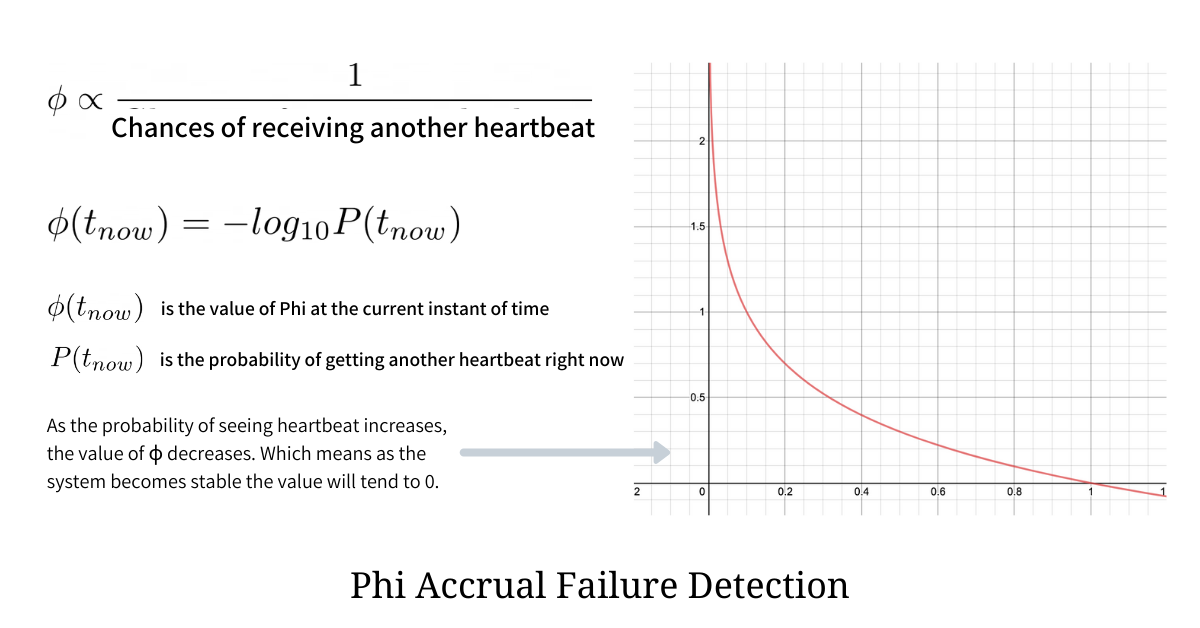
The illustration above mathematically expresses our establishments and shows how we can use -log10(x) function applied to the probability to get a gradual negative slope indicating a decline in the value of φ. We observe how, as the probability of receiving heartbeat increases, the value of φ decreases and approaches 0, and when the probability of receiving heartbeat decreases and approaches 0, the value of φ tends to infinity ∞.
The φ value computed using -log10(x) also suggests our likeliness of making mistakes decreases exponentially as the value of φ increases. So if we say a system is down if φ crosses a certain threshold X where X is 1, it implies that our decision will be contradicted in the future by the reception of a late heartbeat is about 10%. For X = 2, the likelihood of the mistake will be 1%, for X = 3 it will be 0.1%, and so on.
Estimating the probability of receiving another heartbeat
Now that we have defined what φ is, we need a way to compute the probability of receiving another heartbeat given we have seen some heartbeats before. This probability is proportional to the probability that the heartbeat will arrive more than t units after the previous one i.e. longer the wait lesser are the chances of receiving the heartbeat.
In order to implement this, we keep a sampled Sliding Window holding arrival times of past heartbeats. Whenever a new heartbeat arrives, its arrival time is stored into the window, and the data regarding the oldest heartbeat is deleted.
We observe that the arrival intervals follow a Normal Distribution indicating most of the heartbeats arrive within a specific range while there are a few that arrive late due to various network or system conditions. From the information stored in the window, we can easily compute the arrival intervals, mean, and variance which we require to estimate the probability.
Since arrival intervals follow a Normal Distribution, we can integrate the Probability Density Function over the interval (t, ∞) to get the probability of receiving heartbeat after t units of time. Thus the expression for deriving this can be illustrated below.
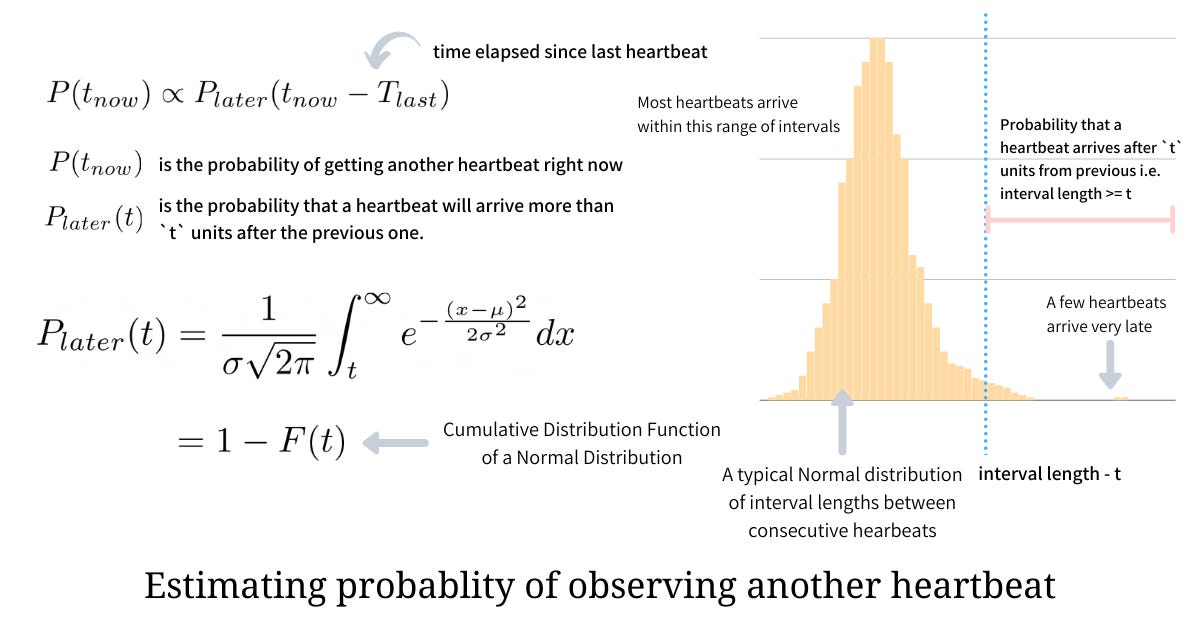
We observe that if the process actually crashes, the value is guaranteed to accrue (accumulate) over time and will tend to infinity ∞. Since the accrual failure detectors output value in a continuous range, we need to explicitly define thresholds crossing which we say that the system crashed.
Benefits of using Accrual Failure Detectors
We can define multiple thresholds, crossing which we can take precautionary measures defined for it. As the threshold becomes steeper the action could become more drastic. Another major benefit of using this system is that it favors a nearly complete decoupling between application requirements and monitoring as it leaves the applications to define threshold according to their QoS requirements.
References
Other articles that you might like
If you liked what you read, consider subscribing to my weekly newsletter at arpitbhayani.me/newsletter where, once a week, I write an essay about programming languages internals, or a deep dive on some super-clever algorithm, or just a few tips on building highly scalable distributed systems.
You can always find me browsing through twitter @arpit_bhayani.


